Un nuovo metodo di modellazione di stacking bayesiano non negativo per prevedere la sopravvivenza del cancro utilizzando dati omici ad alta dimensione Metodologia della ricerca medica BMC

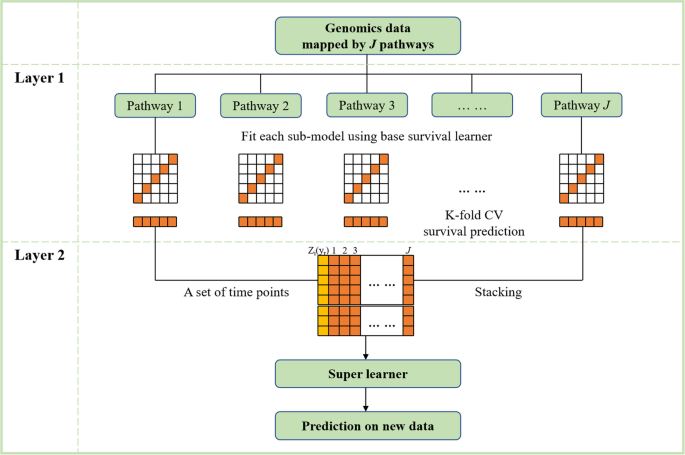
Strategia di impilamento di sopravvivenza basata sul percorso

Supponiamo che i dati sulla sopravvivenza siano correttamente censurati N Gli argomenti sono costituiti da terzine {(sì_IO, δ_IO,S_IO)},l IO= 1, 2, …, N. Indica il tempo di sopravvivenza osservatosì_IO= minuto( R_IO, C_IO), Dove R_IO EC_IO sono rispettivamente l'ora dell'evento e l'ora della censura. δ_IO= IO ( R_IO<C_IO) indica il verificarsi di eventi. L'obiettivo è stimare la funzione di sopravvivenza della variabile casuale evento-tempoY Dipende SCovariate SQualunque S( sì|S) = S(Y > sì |S). In questo studio, miriamo a prevedere la sopravvivenza dei pazienti affetti da cancro utilizzando dati genomici.

Il metodo di survival stacking proposto è un'architettura di apprendimento a due livelli composta da più studenti di base (sottomodelli) e uno studente distinto (metamodello). Vedere la Figura 1 per il flusso del frame.

Per prima cosa trasformiamo i dati del genoma inCSottodati contenenti geni in ciascun percorso. Quindi, nel primo livello, i sottomodelli vengono addestrati in modo indipendente per ciascun sottodato. I sottomodelli risultanti rappresentano il potere predittivo delle traiettorie. Per mitigare il sovradattamento, calcoliamo i predittori di sopravvivenza con convalida incrociata basati sui sottomodelli. Nello specifico, in ogni passaggio, i campioni di dati originali vengono divisi in modo casuale KSottogruppi (pieghe) di uguale dimensione (approssimativa). IL K^sì La piega viene utilizzata come dati di convalida, Quinto(K), mentre le restanti pieghe sono i dati di allenamento,T(-K),K= 1, 2, …, K . Nei dati di addestramento è possibile utilizzare un modello di penalità di Cox per adattare il sottomodello e i rischi sottostantiH₀^{– K}( sì^–K) può essere stimato con il metodo di Breslow. Quindi il predittore lineare (lp^K) nei dati di validazione sono stimati dal sottomodello adattato. Probabilità di sopravvivenza stimate \({\hat {S}}^k\left({y}^k|\boldsymbol{x}\right)\) InQuinto ( K ) può essere calcolato utilizzandolp^K EH₀^–K( sì^{– K}), quello

Dove \({H}^{-k}\left({y}^{-k}\right)={H}_0^{-k}\left({y}^{-k}\right)\times {e}^{l^k}\), \({H}_0^{-k}\sinistra({y}^{-k}\destra)\) È il rischio cumulativo di base, cioè parte integrante del H₀^{– K}( sì^{– K}). Il processo si ripete per tutti K pieghe, producendo probabilità di sopravvivenza predittiva CV per tutti i casi. A C Sottomodelli che possiamo ottenere C Predizioni \({{\hat{S}}_j}^{CV}\left(y|\boldsymbol{x}\right)=\sum_{k=1}^K{{\hat{S}}_j}^ k\sinistra({y}^k|\boldsymbol {x}\right),\kern0.5em j=1,2,\dots, J\). Il secondo livello utilizza uno studente distinto per soddisfare le aspettative di sopravvivenza del CV C Sottomodelli su una serie di punti temporali. I coefficienti risultanti sono i pesi stimati \({\hat{w}}_j\) ACSottomodelli. Funzione di sopravvivenza predittiva \(\hat {S}\left(y|\boldsymbol {x}\right)\) Può essere stimato combinando i predittori CSottomodelli \({\hat{S}}_j\left(y|\boldsymbol{x}\right)\) (Rinnova i dati originali) utilizzando i pesi \({\hat{w}}_j\).

Metodo di stima dei pesi \({\hat{w}}_j\)

Approccio di combinazione lineare

Tipicamente, la funzione di sopravvivenza è predittiva \(\hat {S}\left(y|\boldsymbol {x}\right)\) È una combinazione lineare di predittori C Sottomodelli candidati indicati come:

Miglioriamo i pesi \(\che{w}\) Riducendo la perdita della sindrome dell'intestino irritabile. Un’altra funzione di perdita, come la perdita basata sull’AUC, dovrebbe essere un’alternativa adeguata [22]. L'IBS misura la distanza quadrata tra probabilità ed eventi osservati in un insieme di punti nel temposì₁,…,sì_S [23]che può essere scritto come,

Dove R( sì_S) rappresenta i pazienti che in quel momento sono ancora a rischio sì_S, G_IO(sì_S) = IO( sì_IO> sì_S). Possiamo stimare \(\che{w}\) Riducendo l’incidenza della sindrome dell’intestino irritabile. Pesi generalmente stimati \({\hat{w}}_j\) Vincolato dalla non negatività per una varianza inferiore e una migliore previsione. Questo vincolo può essere ottenuto utilizzando un algoritmo di ottimizzazione non lineare basato sul metodo di Lagrange aumentato che può essere implementato in una funzione R. solnp [24]. Per quanto riguarda la scelta delle fasce orarie sì₁,…, sì_Sutilizziamo nove quantità equidistanti per distribuire gli eventi osservati come chiamato da Andrew Way [19].

Approccio combinato bayesiano

Oltre alle soluzioni IBS, se trattiamo i predittori di sopravvivenza del sottomodello come covariate e trattiamo il caso dipendente dal tempo G_IO( sì_S(0) per morto e 1 per vivo in ogni momento sì_S) Come risultato binario, la sopravvivenza attesa può essere espressa come:

È il modello lineare generalizzato (GLM).H È una funzione di correlazione, come la funzione sigmoidea, per garantire che la probabilità di sopravvivenza attesa sia 0-1.

Lazo non negativo (nLasso)

La progressione della formula (4) è quella che possiamo aggiungere A 1 nel GLM di cui sopra estendendo così l'uso dell'impilamento di sopravvivenza, come ad esempio gestire molti sottomodelli (in uno scenario ad alta dimensione), che è poco pratico per solnp.

È noto che Lasso equivale a un modello gerarchico bayesiano con DE che precede i coefficienti [25]con coefficienti qualificati come non negativi in ​​questo studio,

Dov'è la bilancia,S Controlla il grado di restringimento. Dimensioni più piccole portano a una contrazione più forte, che porta a sottostime Gi_Y Verso lo zero. I pesi montati con nLasso sono dati da,

I pesi di cui sopra possono essere stimati mediante l'algoritmo del rapporto di coordinate periodiche utilizzando com Pacchetto in R. restrizioneGi Essere non passivi può essere facilmente realizzato utilizzando com sfratto.

Spike e lasso lasso non negativi (nsslasso)

Espandiamo anche il DE non negativo prima dell'elevazione non negativa e della miscela della lastra prima del DE (Figura 1 supplementare),

Dove S_Y= (1- γ_Y) S₀ + γ_YS₁ Si chiama parametro dell'intervallo totale. γ_Y è un puntatore ( γ_Y ∈{0, 1}) dopo la distribuzione binomiale; S₀ E S₁ ( S₁ >S₀ > 0) sono i parametri di scala rispettivamente per l'altezza e la distribuzione del solaio.S₁ Applica una compressione più debole a percorsi di effetti più forti e solitamente è fissato su un valore maggiore, ad esS₁ = 1; Mentre S₀Fornisce una compressione più forte ai percorsi di influenza deboli (o addirittura una compressione a zero) ed è un valore flessibile più piccolo scelto da un insieme di valori candidati predeterminati tramite convalida incrociata. Il lazo a punta e lastra è solitamente più adattabile del lazo [26]. I pesi possono essere stimati mediante l'algoritmo del rapporto di coordinate EM [26] utilizzandocompacchetto eBahjalam pacchetto in R. È anche possibile vincolare i pesi affinché siano non negativi utilizzandocomsfratto.

Rete neurale artificiale

Dato che la ANN può agire come un classificatore e dare pesi vincolati (non negativi) ai dati di input, possiamo usarla come studente discriminante. L'ANN utilizza l'algoritmo di propagazione all'indietro e l'algoritmo di discesa del gradiente per stimare iterativamente i pesi.

Valutare le prestazioni del modello

In linea di principio, il modello di survival stacking è un problema di classificazione binaria per un dato periodo [21]. In questo caso abbiamo utilizzato l'AUC dipendente dal tempo e il punteggio Brier (BS) dipendente dal tempo, che calcola l'AUC e il BS per gli organismi in un gruppo a rischio in qualsiasi momento, come raccomandato da Robert Tibshirani. [21]. L'AUC dipendente dal tempo viene utilizzata per esaminare la capacità del modello di discriminare tra diversi risultati in un dato momento. La BS dipendente dal tempo viene utilizzata per misurare le prestazioni di una calibrazione in un dato momento: \(\textrm{BS}(y)=\frac{1}{n}\sum_{i=1}^n{\left({Z}_i(y)-\hat{S}\left(y| \boldsymbol {x}\right)\right)}^2\). Abbiamo scelto tre punti temporali da valutare, ovvero il 25, 50 e 75% del tempo totale di osservazione dei dati del test.

Metodi statistici competitivi

Nel modello di impilamento di sopravvivenza da noi proposto, Lasso Cox è stato utilizzato per costruire sottomodelli basati sul percorso. Per unire i sottomodelli, abbiamo utilizzato solnp (implementato dalla funzione Rsolnp), nLasso/nsslasso (implementato nel pacchettocomEBahjalam) e una ANN (implementata utilizzando la libreria TensorFlow (2.3.0) di Python (3.7) e i pesi possono essere vincolati a non negativi utilizzando kernel_constraint = Non_neg()) come studenti distinti. Vedere il processo di sintesi ANN, Figure supplementari 2 e 3. Per i punti temporali, abbiamo utilizzato nove quantità equidistanti per la distribuzione degli eventi osservati, vale a dire {0, 0,125, 0,25, 0,375, 0,5, 0,625, 0,75, 0,875, 1}. Confrontiamo le prestazioni del nostro metodo proposto con diversi metodi esistenti a modello singolo, inclusa la regressione Lasso Cox ampiamente utilizzata (com) [27] Ed estensioni che includono strutture di gruppo: Group Lasso (gsslasso) (Bahjalam) [28]lazo del gruppo nidificato (grlasso), cMCP del gruppo nidificato e deviazione assoluta con taglio uniforme del gruppo nidificato (grSCAD) (grpregOverlap) [29]. Le prestazioni di questi metodi sono state valutate utilizzando dati simulati e reali. Tutti i metodi a modello singolo vengono implementati utilizzando parametri predefiniti. Tutte le analisi sono state eseguite utilizzando il software R (4.1.3).CPU Dell T7920 Intel Windows 10 Gold 5117 a 2,00 GHz.